◆ gnuplot マニュアルの PDF 日本語版 :
10 月 21 日付けで マニュアルの PDF 日本語版 (2003/10/21; 603,956 bytes) も更新されていますので、ここに紹介させていただきます。
この PDF 日本語版は正式には gnuplot 3.7.3 用ではありませんが、 gnuplot 3.7.2 とは殆んど違いはありませんので、 必要な時には上記の日本語版ヘルプファイルを参照されたら良いだろうと 思います。
ここで、Windows において PDF ファイルのダウンロード方法は、 右クリックにて 『 対象をファイルに保存 』 を選択 してください。 そして、 この PDF ファイルの gp372-20031021.pdf は Acrobat Reader ( 最新版 では Adobe Reader とよぶ ) にてお読みください。
▲ Gnuplot
(2)
gnuplot の基本事項
gnuplot の起動と終了 :
デスクトップ上の gnuplot のショートカットアイコンを
ダブルクリックすると gnuplot が起動する。
終了は、gnuplot の起動画面にて、
次のようにコマンド入力してから Enter キーを押してください :
gnuplot> exit
または
gnuplot> quit
演算子 : 四則演算の記号はそれぞれ +, -, *, / である。 ベキを表す記号は ** であり、例えば x の 5 乗は x**5 のように入力する。 なお、円周率の記号のパイは pi にて表すことに注意しておく。
関数 :
関数を表す記号は普通に利用できる。 三角関数は sin, cos, tan などで、 対数関数は log である。
また、平方根は sqrt にて表して、 絶対値は abs にて表わす。
利用できる関数の一覧 :
gnuplot の起動画面での ツール・バーより Functions を クリックする と理解できます。
例 :
三角関数の sin x, cos x, tan x は sin(x), cos(x), tan(x) であり、 log x は log(x) である。 ただ注意すべき点は、 自然対数の底の e が入る関数は exp で表して、例えば指数関数 e^{x} は exp(x) にて表示する。 また x の 平方根は sqrt(x) のように、 x の絶対値 |x| は abs(x) のように入力する。
▲ Gnuplot
(3)
gnuplot での曲線の描き方
これから y=f(x) であらわされる曲線の描画に ついての学習をする。
この時の、曲線の描画コマンドは plot です。
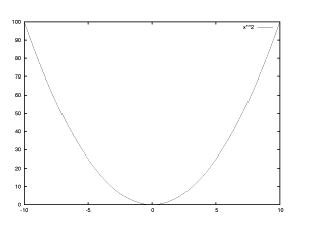 【 練習問題 1 】
【 練習問題 1 】曲線 y=f(x)=x^{2} の描画をする。 標準の範囲は -10 ≦ x ≦ 10 です。
gnuplot> plot x**2
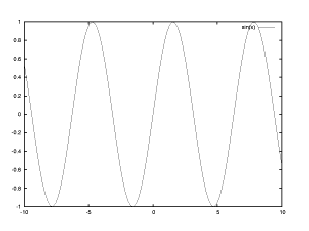 【 練習問題 2 】
【 練習問題 2 】曲線 y=f(x)=sin x の描画をする。
gnuplot> plot sin(x)
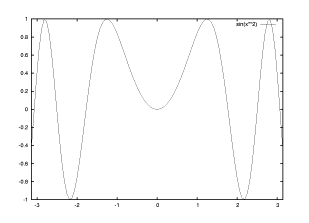 【 練習問題 3 】
【 練習問題 3 】曲線 y=f(x)=sin (x^{2}) を -pi ≦ x ≦ pi の 範囲 にて描画をする。
gnuplot> plot [-pi:pi] sin(x**2)
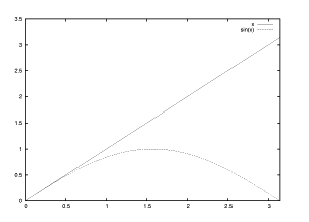 【 練習問題 4 】
【 練習問題 4 】2 曲線 y=f(x)=x と sin x を 0 ≦ x ≦ pi の範囲にて 同時に描画 をする。
gnuplot> plot [0:pi] x, sin(x)
★ Remark :
上記の x と sin(x) の間に入っている , は カンマ であり、ピリオドではありませんので入力時には注意してください。 以下の 入力においても同様の注意が必要です。
 【 練習問題 5 】
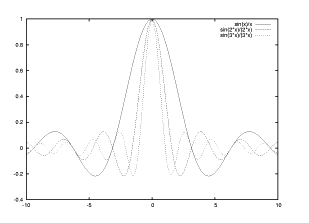
【 練習問題 5 】3 曲線 y=f(x)=sin x/x, sin 2x/2x および sin 3x/3x を -10 ≦ x ≦ 10 かつ -0.4 ≦ y ≦ 1 の範囲にて同時に描画をする。
gnuplot> plot [-10:10][-0.4:1] sin(x)/x, sin(2*x)/(2*x), sin(3*x)/(3*x)
以上の実習の後に TeX 文書への gnuplot での描画の取り込み方法 の解説を行なってから、時間内で作成できる次のような課題を提出した :
【 今 日 ( 5 月 9 日 ) の 課 題 】
gnuplot にて練習問題での曲線以外のものを自分自身 で描いて、その曲線を TeX 文書に取り込んだ文書 ( 感想文を含む ) を作成 しなさい。
以下は、講義の時間内に作成して提出された 作品の一部と感想です。
山田 裕子さんの作品 :
初めは、すごく複雑な数式をグラフにするなんて、 すごく難しいだろうなあと思っていたけれど、 ただ式を打つだけで簡単にできたのでビックリしました。
それと同時に感動しました。 何度も何度も違ったグラフを 書くのも楽しかったです。
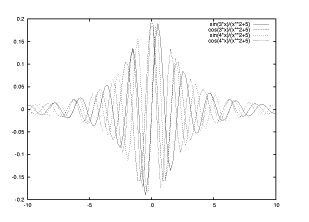
このグラフは y=f(x)= sin 3x/(x^{2}+5), cos 3x/(x^{2}+5), sin 4x/(x^{2}+5), cos 4x/(x^{2}+5) なる 4 つの関数の同時描画です。
何も考えずただ適当に考えて作ったグラフですが、 私はとっても満足できました。 数式や、グラフを少し書けるように なってなんだか新鮮なのと同時にうれしいです!
gnuplot> plot sin(3*x)/(x**2+5), cos(3*x)/(x**2+5), sin(4*x)/(x**2+5), cos(4*x)/(x**2+5)
齋藤 俊輔君の作品 : gnuplot smile
abs コマンドを試しに使ってみたら使えたので、 絶対値を使った曲線を描いてみました。
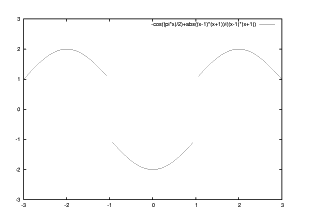
この関数は y=f(x)= -cos ((pi*x)/2) + |(x-1)(x+1)|/(x-1)(x+1) です。
多分、笑っている顔のように見えると思います。 ( ただし、x の範囲を -3 ≦ x ≦ 3 に限定しないといけませんが。)
複雑なグラフは、手書きだと面倒だし、頭の中で創造するのも難しいです。
ところが、gnuplot を使えば、パソコンでグラフを描いて、さらにそれを印刷 できるじゃないですか! それならば、グラフを使った問題やワークシートなどを 作れるので、非常に便利だと思います。
★ 第(1)項で紹介しました新潟工科大学の竹野研究室主幹の竹野茂治先生は、 この曲線をご覧になって 齋藤君の作品を gnuplot smile と名付けてくださいました。 gnuplot においての gnuplot smile への入力は次のようにします :
gnuplot> plot [-3:3] [-3:3] -cos((pi*x)/2)+abs((x-1)*(x+1))/((x-1)*(x+1))
今日の課題に関しては、各自で良く考えられたユニークな曲線が数多く 提出されてありました。
▲ Gnuplot
(4) gnuplot での曲面の描き方
これから z=f(x,y) であらわされる曲面、および高度なグラフの描画についての 学習をする。
Part 1. z=f(x,y) であらわされる曲面の描画
この時の、曲面の描画コマンドは splot です。
 【 練習問題 6 】
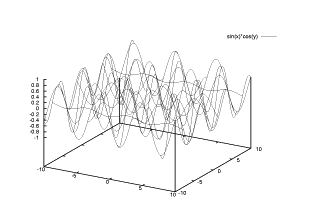
【 練習問題 6 】曲面 z=f(x,y)=sin x cos y の描画をする。 標準の範囲は -10 ≦ x ≦ 10 および -10 ≦ y ≦ 10 です。
gnuplot> splot sin(x)*cos(y)
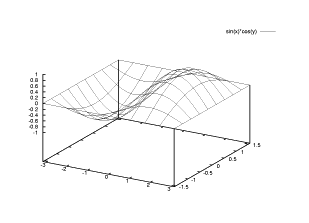 【 練習問題 7 】
【 練習問題 7 】曲面 z=f(x,y)=sin x cos y の描画をする。 範囲 は - pi ≦ x ≦ pi および - pi/2 ≦ y ≦ pi/2 です。
gnuplot> splot [-pi:pi] [-pi/2:pi/2] sin(x)*cos(y)
| set hidden3d | 隠 線 処 理 |
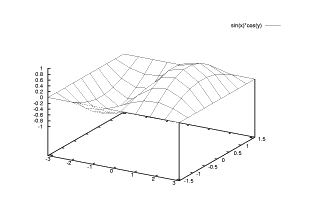 【 練習問題 8 】
【 練習問題 8 】曲面 z=f(x,y)=sin x cos y を - pi ≦ x ≦ pi および - pi/2 ≦ y ≦ pi/2 の範囲にて、 隠線処理 ( 本来は隠れて見えないはずの曲面や軸を表示しない ) を行ってから 描画をする。
gnuplot> set hidden3d
gnuplot> splot [-pi:pi] [-pi/2:pi/2] sin(x)*cos(y)
| set isosamples 50 | 曲面を表示する線の数を 50 本 |
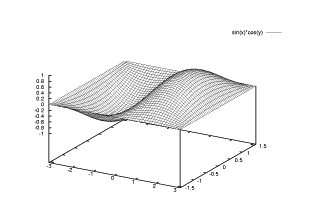 【 練習問題 9 】
【 練習問題 9 】
曲面 z=f(x,y)=sin x cos y を - pi ≦ x ≦ pi および - pi/2 ≦ y ≦ pi/2 の範囲にて、隠線処理かつ 曲面を表示する線の数 ( 標準値は 10 本 )を 50 本 にしてから描画をする。
gnuplot> set hidden3d
gnuplot> set isosamples 50
gnuplot> splot [-pi:pi] [-pi/2:pi/2] sin(x)*cos(y)
【 演 習 問 題 】
z = f(x,y) = sin(sqrt(x^2 + y^2))/sqrt(x^2 + y^2) で定まる曲面の図を 標準の範囲において、隠線処理かつ曲面を表示する線の数を 50 本にしてから 描画をしてください。( これは、昨年の基礎数学演習において学習した曲面 )
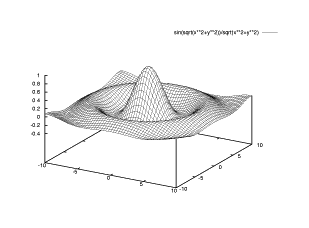 【 解 答 】
【 解 答 】gnuplot> set hidden3d
gnuplot> set isosamples 50
gnuplot> splot sin(sqrt(x**2+y**2))/sqrt(x**2+y**2)
Part 2. 高度なグラフの作成
はじめに、媒介変数を使った関数のグラフを描いてみます。 ここで、 媒介変数モードでの 2 次元グラフの 媒介変数 t を用います。
| set parametric | 媒介変数モードに設定する |
 【 練習問題 10 】
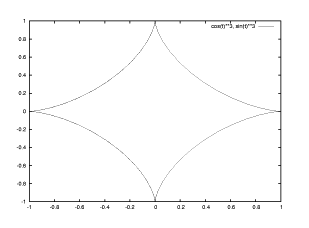
【 練習問題 10 】アステロイド曲線 x=(cos t)^{3}, y=(sin t)^{3} の 描画をするには、次のように入力します。
gnuplot> set parametric
gnuplot> plot cos(t)**3, sin(t)**3
| set trange [a:b] | 変数 t の範囲が a ≦ t ≦ b |
| set size ratio 0.3 | x 軸と y 軸の長さの比率が 0.3 |
 【 練習問題 11 】
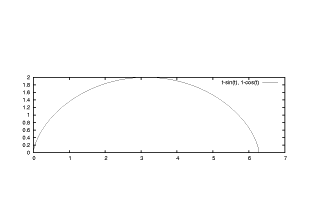
【 練習問題 11 】サイクロイド曲線 x=t - sin t, y=1 - cos t の描画 をする。 範囲は 0 ≦ t ≦ 2pi であり、x 軸と y 軸の長さの比率が 0.3 として ください。
gnuplot> set parametric
gnuplot> set trange [0:2*pi]
gnuplot> set size ratio 0.3
gnuplot> plot t-sin(t), 1-cos(t)
続いて、媒介変数モードで 3 次元のグラフを作成する場合には、 媒介変数 u, v を用います。
 【 練習問題 12 】
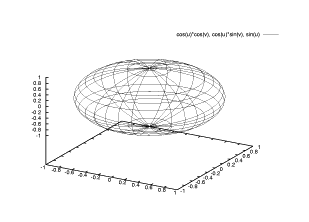
【 練習問題 12 】球面 x=cos u cos v, y=cos u sin v, z=sin u の描画 をするには、次のように入力します。
gnuplot> set parametric
gnuplot> splot cos(u)*cos(v), cos(u)*sin(v), sin(u)
最後に、r=f(t) で表わされる 2 次元のグラフの 極座標表示 を考察することにします。
| reset | すべての設定を デフォルトに戻す |
gnuplot> reset
| set polar | 2 次元のグラフの極座標表示 |
 【 練習問題 13 】
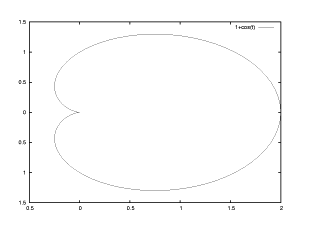
【 練習問題 13 】カージオイド曲線 r=1 + cos t の描画をする。 標準の範囲は 0 ≦ t ≦ 2pi です。
gnuplot> set polar
gnuplot> plot 1+cos(t)
以上の実習の後に、前回と同様 TeX 文書への gnuplot での描画の取り込み方法 の解説を行なってから、時間内で作成できる次のような課題を提出した :
【 今 日 ( 5 月 16 日 ) の 課 題 】
gnuplot にて練習問題以外の曲面を一つ、および 媒介変数モードまたは極座標表示を利用した描画を一つの合計 2 個を TeX 文書 に取り込んだ文書 ( 感想文を含む ) を作成しなさい。
以下は、講義の時間内に作成して提出された 作品の一部と感想です。
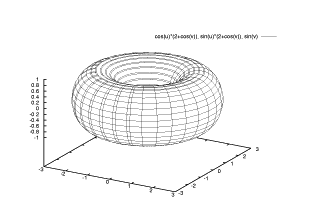
河村 規代花さんの作品 :
今日の授業では、とても数学科っぽいグラフを書くことができた気分です。 まず は、グラフの説明をしたいと思います。
この曲面は x=cos u (2 + cos v), y=sin u (2 + cos v), z=sin v です。
おなかがすいたので、ドーナツ型の図形を描いてみました。
今日も楽しかったです。
gnuplot> set parametric
gnuplot> set hidden3d
gnuplot> set isosamples 50
gnuplot> splot cos(u)*(2+cos(v)), sin(u)*(2+cos(v)), sin(v)
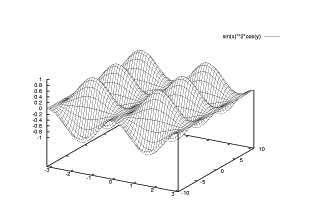
後藤 俊明君の作品 :
今日は gnuplot で曲面や媒介変数を使った関数のグラフ、極座標表示のグラフ を描くことができた。
この関数は z=f(x,y)=(sin x)^{2} cos y です。
曲面なんて、フリーハンドで描くのは 限界があるしわかりづらい。 去年の基礎数学演習 の授業でも、曲面や接平面がでてきて理解に苦しんだが、このようにグラフで表して 目で見ることができていれば、もっとわかりやすかったのではないだろうか。
曲面を自分で描けたときは、すごくうれしかった。
gnuplot> set hidden3d
gnuplot> set isosamples 50
gnuplot> splot [-pi:pi] sin(x)**2*cos(y)
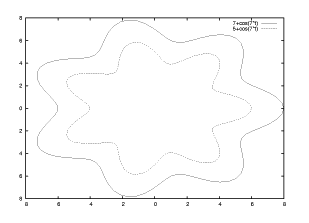
宗宮 由実さんの作品 :
極座標表示での曲線は r=7 + cos 7t と r=5 + cos 7t の曲線を同時に描画しました。
これは、最近私が好きなドーナツの形に似せて作り 上げました。 上手くできたので、満足です。
カージオイドやサイクロイドはもちろん他の曲線も、 すごく綺麗な曲線であらわすことができ、感動しました。
去年、先生が下さったプリントの曲面も自分で 作ることができ、やりきった感触です。
gnuplot> set polar
gnuplot> plot 7+cos(7*t), 5+cos(7*t)
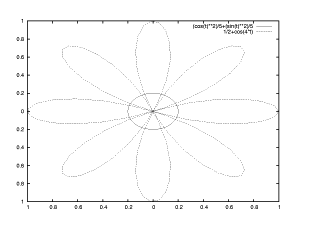
野崎 江美さんの作品 :
極座標表示で 半径 1/5 の円と r=1/2 + cos 4t のグラフ を組み合わせて、お花を書いて見ました!
普段、教科書などで数式を見ても、 それがいったいどんなグラフなのか想像できず、問題などを 解いていてもいまいちパッとしませんでした。 でも、gnuplot を 使うと、立体の曲面でも目で見ることができるので楽しいです。
数学の授業でも、このようにパソコンでいろいろなグラフを見ることができれば、 数学の授業がもっともっと楽しくなるんじゃないかなぁ・・・と思いました!
gnuplot> set polar
gnuplot> plot (cos(t)**2)/5+(sin(t)**2)/5, 1/2+cos(4*t)
今回の課題に関しても、各自で良く考察されたユニークな曲線および曲面が 数多く提出されてありました。
来週 ( 5 月 23 日 ) は学園祭のために休講となるので、次のような レポート課題を提出した。
【 レ ポ ー ト 問 題 】
数学の問題と解答例を TeX を用いて 作成しなさい。 gnuplot が利用できるならば、 作成した図を TeX 文書に取り込むと良い。
大学入試程度の問題から、1 枚の A4 用紙全体を利用して作成してください。
提出は再来週 5 月 30 日 (金) の授業の時です。
参考 : 学生は、ノート・パソコンを大学入学時に購入して持っています。 ですから、 家でも学習はできます。
このレポート課題に対しても、優秀な力作が数多く提出されており 採点していて嬉しい限りであった。
▲ Gnuplot
(5)
gnuplot での描画への補足事項
先日の
レポート課題
において、
『
gnuplot の描画でタイトル名の記述および x 軸、y 軸、z 軸の
ラベル、そして x 軸と y 軸の表示は可能なのか?
』
の質問が多く寄せられたので、6 月 6 日 (金) に次のような解説を
プリントにして配布してみました。
gnuplot 3.7.3 では、英語による表示は以下のようなコマンド入力にて 可能です。 しかしながら日本語については、日本語表示の対応が なされてないので無理です。
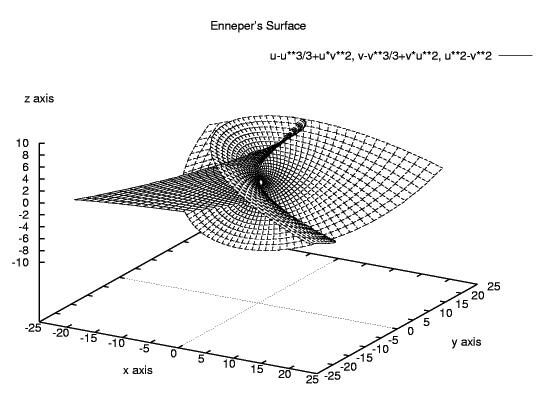
これから、媒介変数 u と v を用いる媒介変数モードにて有名な エネパーの曲面 ( Enneper's Surface )
x=u - u^{3}/3 + uv^{2},
y=v - v^{3}/3 + vu^{2},
z=u^{2} - v^{2}
を例に取りながら、以下の描画の入力例で説明します :
| set title "Enneper's Surface" | タ イ ト ル 名 の 記 述 |
| set xlabel "x axis" | x 軸にラベル x axis を表示 |
| set xzeroaxis | x 軸 を 点 線 で 表 示 |
| set urange [a:b] | 変数 u の範囲が a ≦ u ≦ b |
gnuplot> set title "Enneper's Surface"
gnuplot> set parametric
gnuplot> set hidden3d
gnuplot> set isosamples 50
gnuplot> set xlabel "x axis"
gnuplot> set ylabel "y axis"
gnuplot> set zlabel "z axis"
gnuplot> set xzeroaxis
gnuplot> set yzeroaxis
gnuplot> set urange [-3:3]
gnuplot> set vrange [-3:3]
gnuplot> splot u-u**3/3+u*v**2, v-v**3/3+v*u**2, u**2-v**2
▲ Gnuplot
(6)
TeX 文書への gnuplot での描画の取り込み方法
これから
TeX 文書へ描画を取り込む方法について
述べてみます。
ここでは、 dviout for Windows の活用 を前提として考えますので、 Ghostscript のインストール も既になされていると仮定して話を進めていきます。
具体例として、正規分布曲線 y=f(x)=exp(-x^{2}) を TeX 文書に取り込む方法を 述べます。
まず、曲線 y=f(x)=exp(-x^{2}) を -3 ≦ x ≦ 3 の範囲にて gnuplot で描いた図を準備します。 このために、次のような順序の入力にて、例えば フォルダ temp 内に EPS ファイル の mytest.eps として保存します ( ここで、 EPS ファイル名は 半角の英数字が望ましく mytest.509.eps のように ドット . が 2 個以上入ってもいけません。 ) :
| terminal postscript eps | EPS ファイルの出力 |
gnuplot> set terminal postscript eps
gnuplot> set output "c:/temp/mytest.eps"
gnuplot> plot [-3:3] exp(-x**2)
gnuplot> set output
続いて、できた mytest.eps を自分の TeX 文書があるフォルダに移動させます。
そして TeX 文書に次のような記述を追加して
graphicx パッケージに
dviout オプションを指定
してから利用をします。
\documentclass[a4paper,12pt]{jarticle}
\usepackage[dviout]{graphicx}
\begin{center}
\includegraphics{mytest.eps}
\end{center}
\end{document}
図版の大きさの拡大・縮小は、次のように幅 (
width
) で調整することが可能です。 また、オプションの
clip
は、描画領域の外側を描かない ( クリッピングする ) という
指定になっています :
\begin{center}
\includegraphics[width=8cm,clip]{mytest.eps}
\end{center}
上の TeX 原稿を pLaTeX2ε で処理してできる dvi ファイルをもとに
Ghostscript
を利用して EPS ファイルを PBM 形式に変換してから
dviout for Windows
でプレビューおよびプリントアウトを行ない
ます : dviout for Windows による出力例★ 参考事項 :
dviout オプションを利用 するためには、c:\dviout\Graphic\Latex2e 内にある color.cfg, dviout.def, graphics.cfg の 3 個 を c:\usr\local\share\texmf\tex\latex\graphics 内へ コピーしてください ( 注意: 移動ではありません! )。
▲ Gnuplot
(7)
gnuplot への参考文献
私の手元には、次の一冊の書籍があります :
矢吹 道郎 監修、 大竹 敢 著 : 『 使いこなす GNUPLOT (改訂新版) 』 ( テクノプレス、 2000 年 )
Windows および UNIX システムの X Windows 上での gnuplot の利用を前提とした解説書です。この他には、 第(1)項で紹介 しました 日本語化された gnuplot のヘルプファイル および gnuplot マニュアルの PDF 日本語版 が大いに役立つことでしょう。
本書を横に置いて gnuplot を使っているうちに、自由に使いこなせるようになることを 目標とした解説がなされてある好書です。
| Gnuplot △ | ▲ Contents |
|---|

Kohsaku HOTTA
khotta.org